IRRELEVANCE OF THE LAFFER CURVE

“It should be known that at the beginning of the dynasty, taxation yields a large revenue from small assessments. At the end of the dynasty, taxation yields a small revenue from large assessments.”

~ Ibn Khaldun, The Muqaddimah

The Laffer Curve states that if tax rates are increased above a certain level, then tax revenues can actually fall because higher tax rates discourage people from working.

According to the Laffer Curve, At a 0% tax rate, tax revenue would obviously be zero. As tax rates increase from low levels, tax revenue collected by the also government increases. Eventually, if tax rates reached 100 percent, shown as the far right on the Laffer Curve, all people would choose not to work because everything they earned would go to the government and therefore

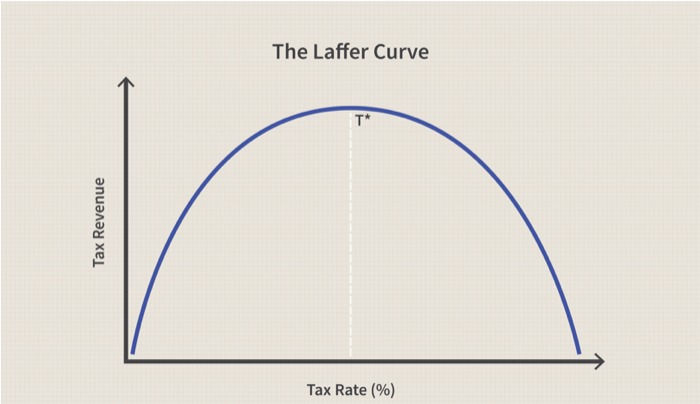
at a 100% tax rate, revenue will still be 0. Therefore it has to be true that at some point in the range where tax revenue is positive, it must reach a maximum point.

This is represented by T* on the graph. To the left of T* an increase in tax rate raises more revenue than is loss to offsetting worker and investor behaviour. Increasing

rates beyond T* however would cause people not to work

as much or not at all, thereby reducing total tax revenue.

Therefore, in theory at any tax rate to the right of T*, a reduction in tax rate will actually increase total revenue. Governments would like to be at point T* because it is the point at which the government collects maximum amount of tax revenue while people continue to work hard. If the current tax rate is to the right of T*, then lowering the tax rate will both stimulate economic growth by increasing incentives to work and invest, and increase government revenue because more work and investment means a larger tax base.

However, Economists disagree on the level at which higher tax rates actually cause disincentives to work. Because in reality, it is more complicated. There are some fundamental problems with the Laffer Curve. notably that it is far too simplistic in its assumptions.

Firstly, the existence and position of T* depends entirely on the shape of the Laffer Curve. The underlying concept of the Laffer Curve only requires that tax revenue be zero at 0% and at 100%, and positive in between. It says nothing about the specific shape of the curve at points in between 0% and 100% or the position of T*. The shape of the actual Laffer Curve might be dramatically different from the simple, single peaked curve commonly depicted. If the curve has multiple peaks, flat spots, or discontinuities, then multiple T*’s might exist. If the curve is skewed deeply to the left or right, T* might occur at extreme tax rates like 1% tax rate or a 99% tax rate, which might put tax revenue maximising policy into serious conflict with social equity or other policy goals. Furthermore, just as the basic concept does not necessarily imply a simply shaped curve, it does not imply that a Laffer Curve of any shape would be static. The Laffer Curve might easily shift and change shape over time, which would mean that to maximise revenue, or just avoid falling revenue, policy makers would have to constantly adjust tax rates.

This leads to the second criticism, that policy makers would be in practice unable to observe the shape of the Laffer Curve, the location of T*, whether multiple T*’s exist, or whether and how the Laffer Curve might shift over time. The only thing policy makers can reliably observe is the current tax rate and associated revenue receipts (and past combinations of rates and revenue). Economists can guess at what the shape might be, but only trial and error could actually reveal the true shape of the curve, and only at those tax rates that are actually implemented. Raising or lowering tax rates might move the rate toward T*, or it might not. Moreover, if the Laffer Curve has any shape other than the assumed simple, single peaked parabola, then tax revenue at points between the current tax rate and T* could have any range of values higher or lower than revenue at the current rate and the same or lower than T*. An increase in tax revenue after a rate change would not necessarily signal that the new rate is closer to T* (nor a decrease in revenue signal that it is further away). Even worse, because tax policy changes are made and applied over time, the shape of the Laffer Curve could shift; policy makers could never know if an increase in tax revenue in response to a tax rate change represented a movement along the Laffer Curve toward T*, or a shift in the Laffer Curve itself, with a new T*. Policy makers trying to reach T* would effectively be groping in the dark after a moving target.

Lastly, it is not clear on economic grounds that maximising or increasing government revenue (by moving toward T* on the Laffer Curve) is even an appropriate goal for choosing tax rates. It might easily be the case that a government could meet the otherwise unmet needs of its citizens and provide any necessary public goods at some level of revenue lower than the maximum it can potentially extract from the economy, perhaps much lower depending on the position of T*. If so, then given the well researched principal agent problems, rent seeking, and knowledge problems that arise with politically driven allocation of resources, putting additional funds in public coffers beyond this socially optimal level might just produce additional unnecessary social costs, inefficiencies, and dead weight losses. Maximising government tax revenue by taxing at T* would also likely maximise these costs. A more appropriate goal might be to reach the minimum tax revenue necessary to achieve only those socially necessary policy goals, which would seem to be almost the exact opposite of the purpose of the Laffer Curve.